Portal:Mathematics

The Mathematics Portal

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Refresh with new selections below (purge)

Featured articles – load new batch

Featured articles are displayed here, which represent some of the best content on English Wikipedia.

Image 1

Noether c. 1900–1910

Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She also proved Noether's first and second theorems, which are fundamental in mathematical physics. Noether was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.

Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
Image 2

Elementary algebra studies which values solve equations formed using arithmetical operations.

Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition and multiplication.

Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)
Image 3

Portrait by August Köhler, c. 1910, after 1627 original

Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.

Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. He is also known for postulating the Kepler conjecture. (Full article...)
Image 4

Hilary Putnam

The Quine–Putnam indispensability argument is an argument in the philosophy of mathematics for the existence of abstract mathematical objects such as numbers and sets, a position known as mathematical platonism. It was named after the philosophers Willard Van Orman Quine and Hilary Putnam, and is one of the most important arguments in the philosophy of mathematics.

Although elements of the indispensability argument may have originated with thinkers such as Gottlob Frege and Kurt Gödel, Quine's development of the argument was unique for introducing to it a number of his philosophical positions such as naturalism, confirmational holism, and the criterion of ontological commitment. Putnam gave Quine's argument its first detailed formulation in his 1971 book Philosophy of Logic. He later came to disagree with various aspects of Quine's thinking, however, and formulated his own indispensability argument based on the no miracles argument in the philosophy of science. A standard form of the argument in contemporary philosophy is credited to Mark Colyvan; whilst being influenced by both Quine and Putnam, it differs in important ways from their formulations. It is presented in the Stanford Encyclopedia of Philosophy: (Full article...)
Image 5
Plots of logarithm functions, with three commonly used bases. The special points $log b b = 1$ are indicated by dotted lines, and all curves intersect in $log b 1 = 0$ .

In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of $1000$ to base $10$ is $3$ , because $1000$ is $10$ to the $3$ rd power: $1000 = 10 3 = 10 \times 10 \times 10$ . More generally, if $x = b y$ , then $y$ is the logarithm of $x$ to base $b$ , written $log b x$ , so $log 10 1000 = 3$ . As a single-variable function, the logarithm to base $b$ is the inverse of exponentiation with base $b$ .

The logarithm base $10$ is called the decimal or common logarithm and is commonly used in science and engineering. The natural logarithm has the number $e \approx 2.718$ as its base; its use is widespread in mathematics and physics because of its very simple derivative. The binary logarithm uses base $2$ and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written $log x$ . (Full article...)
Image 6
High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.

By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
Image 7

Damage from Hurricane Katrina in 2005. Actuaries need to estimate long-term levels of such damage in order to accurately price property insurance, set appropriate reserves, and design appropriate reinsurance and capital management strategies.

An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.

While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in 17th-century studies of probability and annuities. Actuaries in the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems; actuaries use this knowledge to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...)
Image 8
The manipulations of the Rubik's Cube form the Rubik's Cube group.

In mathematics, a group is a set with a binary operation that satisfies the following constraints: the operation is associative, it has an identity element, and every element of the set has an inverse element.

Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called ⁠ $1$ ⁠ (these properties characterize the integers in a unique way). (Full article...)
Image 9

Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American mechanical engineer and scientist who made fundamental theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.

In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history". In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics". (Full article...)
Image 10

Title page of the first edition of Wright's Certaine Errors in Navigation (1599)

Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.

Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)
Image 11
The weighing pans of this balance scale contain zero objects, divided into two equal groups.

In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if $y$ is even then $y + x$ has the same parity as $x$ —indeed, $0 + x$ and $x$ always have the same parity.

Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
Image 12
Logic studies valid forms of inference like modus ponens.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work." Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
$Image 13 Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300). In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC). It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)$

Image 13
Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300).

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers, the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, $21$ is the GCD of $252$ and $105$ (as $252 = 21 \times 12$ and $105 = 21 \times 5)$ , and the same number $21$ is also the GCD of $105$ and $252 - 105 = 147$ . Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, $21 = 5 \times 105 + (-2) \times 252$ ). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)
Image 14

Rejewski, c. 1932

Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.

Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)
Image 15

Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is best known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.

Feynman developed a pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams and is widely used. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)

More featured articles

edit

Selected image – show another

animation showing a roughly star-shaped graph being traced out as a smaller circle rolls around inside of a larger circle

Hypotrochoid

Credit: Sam Derbyshire

A hypotrochoid is a curve traced out by a point "attached" to a smaller circle rolling around inside a fixed larger circle. In this example, the hypotrochoid is the red curve that is traced out by the red point 5 units from the center of the black circle of radius 3 as it rolls around inside the blue circle of radius 5. A special case is a hypotrochoid with the inner circle exactly one-half the radius of the outer circle, resulting in an ellipse (see an animation showing this). Mathematical analysis of closely-related curves called hypocycloids lead to special Lie groups. Both hypotrochoids and epitrochoids (where the moving circle rolls around on the outside of the fixed circle) can be created using the Spirograph drawing toy. These curves have applications in the "real world" in epicyclic and hypocycloidal gearing, which were used in World War II in the construction of portable radar gear and may be used today in 3D printing.

More selected pictures

Good articles – load new batch

These are Good articles, which meet a core set of high editorial standards.

Image 1
A binary tiling in the Poincaré disk model of the hyperbolic plane. Each tile edge lies on a horocycle (shown as circles interior to the disk) or a hyperbolic line (arcs perpendicular to the disk boundary). The horocycles and lines are asymptotic to an ideal point located at the right side of the Poincaré disk.

In geometry, a binary tiling (sometimes called a Böröczky tiling) is a tiling of the hyperbolic plane, resembling a quadtree over the Poincaré half-plane model of the hyperbolic plane. The tiles are congruent, each adjoining five others. They may be convex pentagons, or non-convex shapes with four sides, alternatingly line segments and horocyclic arcs, meeting at four right angles.

There are uncountably many distinct binary tilings for a given shape of tile. They are all weakly aperiodic, which means that they can have a one-dimensional symmetry group but not a two-dimensional family of symmetries. There exist binary tilings with tiles of arbitrarily small area. (Full article...)
Image 2
The red graph is the dual graph of the blue graph, and vice versa.

In the mathematical discipline of graph theory, the dual graph of a planar graph $G$ is a graph that has a vertex for each face of $G$ . The dual graph has an edge for each pair of faces in $G$ that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge $e$ of $G$ has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of $e$ . The definition of the dual depends on the choice of embedding of the graph $G$ , so it is a property of plane graphs (graphs that are already embedded in the plane) rather than planar graphs (graphs that may be embedded but for which the embedding is not yet known). For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

Historically, the first form of graph duality to be recognized was the association of the Platonic solids into pairs of dual polyhedra. Graph duality is a topological generalization of the geometric concepts of dual polyhedra and dual tessellations, and is in turn generalized combinatorially by the concept of a dual matroid. Variations of planar graph duality include a version of duality for directed graphs, and duality for graphs embedded onto non-planar two-dimensional surfaces. (Full article...)
Image 3

Graham in 1998

Ronald Lewis Graham (October 31, 1935 – July 6, 2020) was an American mathematician credited by the American Mathematical Society as "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years". He was president of both the American Mathematical Society and the Mathematical Association of America, and his honors included the Leroy P. Steele Prize for lifetime achievement and election to the National Academy of Sciences.

After graduate study at the University of California, Berkeley, Graham worked for many years at Bell Labs and later at the University of California, San Diego. He did important work in scheduling theory, computational geometry, Ramsey theory, and quasi-randomness, and many topics in mathematics are named after him. He published six books and about 400 papers, and had nearly 200 co-authors, including many collaborative works with his wife Fan Chung and with Paul Erdős. (Full article...)
Image 4

Official portrait, 2014

José Félix Mendieta Villarroel (born 15 November 1958) is a Bolivian politician and trade unionist who served as a member of the Chamber of Deputies from Cochabamba, representing circumscription 28 from 2010 to 2015.

Though educated in pedagogy, Mendieta spent most of his career in commercial driving, climbing the ranks of the sector's trade unions to eventually become general secretary of the Sacaba Mixed Motor Transport Union. Though traditionally conservative, under the leadership of figures like Mendieta, many of the country's drivers' unions were reoriented towards the left. (Full article...)
Image 5
Graph of $log 2 x$ as a function of a positive real number $x$

In mathematics, the binary logarithm ( $log 2 n$ ) is the power to which the number $2$ must be raised to obtain the value $n$ . That is, for any real number $x$ ,
: $x=\log _{2}n\quad \Longleftrightarrow \quad 2^{x}=n.$
For example, the binary logarithm of $1$ is $0$ , the binary logarithm of $2$ is $1$ , the binary logarithm of $4$ is $2$ , and the binary logarithm of $32$ is $5$ .

The binary logarithm is the logarithm to the base $2$ and is the inverse function of the power of two function. There are several alternatives to the $log 2$ notation for the binary logarithm; see the Notation section below. (Full article...)
Image 6
Modus ponens is one of the main rules of inference.

Rules of inference are ways of deriving conclusions from premises. They are integral parts of formal logic, serving as norms of the logical structure of valid arguments. If an argument with true premises follows a rule of inference then the conclusion cannot be false. Modus ponens, an influential rule of inference, connects two premises of the form "if $P$ then $Q$ " and " $P$ " to the conclusion " $Q$ ", as in the argument "If it rains, then the ground is wet. It rains. Therefore, the ground is wet." There are many other rules of inference for different patterns of valid arguments, such as modus tollens, disjunctive syllogism, constructive dilemma, and existential generalization.

Rules of inference include rules of implication, which operate only in one direction from premises to conclusions, and rules of replacement, which state that two expressions are equivalent and can be freely swapped. Rules of inference contrast with formal fallacies—invalid argument forms involving logical errors. (Full article...)
Image 7

Lasker in 1929

Emanuel Lasker (German pronunciation: [eˈmaːnuɛl ˈlaskɐ] ; December 24, 1868 – January 11, 1941) was a German chess player, mathematician, and philosopher. He was the second World Chess Champion, holding the title for 27 years, from 1894 to 1921, the longest reign of any officially recognised World Chess Champion, winning 6 World Chess Championships. In his prime, Lasker was one of the most dominant champions.

His contemporaries used to say that Lasker used a "psychological" approach to the game, and even that he sometimes deliberately played inferior moves to confuse opponents. Recent analysis, however, indicates that he was ahead of his time and used a more flexible approach than his contemporaries, which mystified many of them. Lasker knew contemporary analyses of openings well but disagreed with many of them. He published chess magazines and five chess books, but later players and commentators found it difficult to draw lessons from his methods. (Full article...)
Image 8
Selected witch of Agnesi curves (green), and the circles they are constructed from (blue), with radius parameters $a=1$ , $a=2$ , $a=4$ , and $a=8$ .

In mathematics, the witch of Agnesi (Italian pronunciation: [aɲˈɲeːzi, -eːsi; -ɛːzi]) is a cubic plane curve defined from two diametrically opposite points of a circle.

The curve was studied as early as 1653 by Pierre de Fermat, in 1703 by Guido Grandi, and by Isaac Newton. It gets its name from Italian mathematician Maria Gaetana Agnesi who published it in 1748. The Italian name la versiera di Agnesi is based on Latin versoria (sheet of sailing ships) and the sinus versus.
This was read by John Colson as l’avversiera di Agnesi, where avversiera is translated as "woman who is against God" and interpreted as "witch". (Full article...)
Image 9
An arc diagram of the Goldner–Harary graph. This graph has no Hamiltonian cycle, but can be made Hamiltonian by subdividing the edge crossed by the red dashed line segment and adding two edges along this segment.

An arc diagram is a style of graph drawing, in which the vertices of a graph are placed along a line in the Euclidean plane and edges are drawn using semicircles or other convex curves above or below the line. These drawings are also called linear embeddings or circuit diagrams.

Applications of arc diagrams include information visualization, the Farey diagram of number-theoretic connections between rational numbers, and diagrams representing RNA secondary structure in which the crossings of the diagram represent pseudoknots in the structure. (Full article...)
Image 10
In geometry, the Dehn invariant is a value used to determine whether one polyhedron can be cut into pieces and reassembled ("dissected") into another, and whether a polyhedron or its dissections can tile space. It is named after Max Dehn, who used it to solve Hilbert's third problem by proving that certain polyhedra with equal volume cannot be dissected into each other.

Two polyhedra have a dissection into polyhedral pieces that can be reassembled into either one, if and only if their volumes and Dehn invariants are equal. Having Dehn invariant zero is a necessary (but not sufficient) condition for being a space-filling polyhedron, and a polyhedron can be cut up and reassembled into a space-filling polyhedron if and only if its Dehn invariant is zero. The Dehn invariant of a self-intersection-free flexible polyhedron is invariant as it flexes. Dehn invariants are also an invariant for dissection in higher dimensions, and (with volume) a complete invariant in four dimensions. (Full article...)
Image 11
In graph theory, a cop-win graph is an undirected graph on which the pursuer (cop) can always win a pursuit–evasion game against a robber, with the players taking alternating turns in which they can choose to move along an edge of a graph or stay put, until the cop lands on the robber's vertex. Finite cop-win graphs are also called dismantlable graphs or constructible graphs, because they can be dismantled by repeatedly removing a dominated vertex (one whose closed neighborhood is a subset of another vertex's neighborhood) or constructed by repeatedly adding such a vertex. The cop-win graphs can be recognized in polynomial time by a greedy algorithm that constructs a dismantling order. They include the chordal graphs, and the graphs that contain a universal vertex. (Full article...)
Image 12
Schematic representation of the Dirac delta function by a line surmounted by an arrow. The height of the arrow is usually meant to specify the value of any multiplicative constant, which will give the area under the function. The other convention is to write the area next to the arrowhead.

In mathematical analysis, the Dirac delta function (or $δ$ distribution), also known as the unit impulse, is a generalized function on the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. Thus it can be represented heuristically as

$\delta (x)={\begin{cases}0,&x\neq 0\\{\infty },&x=0\end{cases}}$ (Full article...)

More good articles

Did you know (auto-generated) – load new batch

... that people in Madagascar perform algebra on tree seeds in order to tell the future?
... that Ewa Ligocka cooked another mathematician's goose?
... that Green Day's "Wake Me Up When September Ends" became closely associated with the aftermath of Hurricane Katrina?
... that the word algebra is derived from an Arabic term for the surgical treatment of bonesetting?
... that despite a mathematical model deeming the ice cream bar flavour Goody Goody Gum Drops impossible, it was still created?
... that the British National Hospital Service Reserve trained volunteers to carry out first aid in the aftermath of a nuclear or chemical attack?
... that Latvian-Soviet artist Karlis Johansons exhibited a skeletal tensegrity form of the Schönhardt polyhedron seven years before Erich Schönhardt's 1928 paper on its mathematics?
... that ten-sided gaming dice have kite-shaped faces?

edit

More did you know – view different entries

Did you know...

… that the best known lower bound for the length of the smallest superpermutation was first posted anonymously to the internet imageboard 4chan?
...that the mathematician Grigori Perelman was offered a Fields Medal in 2006, in part for his proof of the Poincaré conjecture, which he declined?
...that a regular heptagon is the regular polygon with the fewest sides which is not constructible with a compass and straightedge?
...that the regular trigonometric functions and the hyperbolic trigonometric functions can be related without using complex numbers through the Gudermannian function?
...that the Catalan numbers solve a number of problems in combinatorics such as the number of ways to completely parenthesize an algebraic expression with n+1 factors?
...that a ball can be cut up and reassembled into two balls, each the same size as the original (Banach-Tarski paradox)?
...that it is impossible to devise a single formula involving only polynomials and radicals for solving an arbitrary quintic equation?

More did you know facts

Showing 7 items out of 75

edit

Selected article – show another

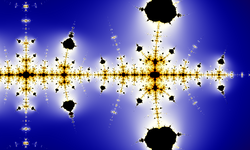Fractals arise in surprising places, in this case, the famous Collatz conjecture in number theory.
Image credit: Pokipsy76

A fractal is "a rough or fragmented geometric shape that can be subdivided in parts, each of which is (at least approximately) a reduced-size copy of the whole". The term was coined by Benoît Mandelbrot in 1975 and was derived from the Latin fractus meaning "broken" or "fractured".

A fractal as a geometric object generally has the following features:

It has a fine structure at arbitrarily small scales.
It is too irregular to be easily described in traditional Euclidean geometric language.
It is self-similar (at least approximately or stochastically).
It has a Hausdorff dimension which is greater than its topological dimension (although this requirement is not met by space-filling curves such as the Hilbert curve).
It has a simple and recursive definition.

Because they appear similar at all levels of magnification, fractals are often considered to be infinitely complex (in informal terms). Natural objects that approximate fractals to a degree include clouds, mountain ranges, lightning bolts, coastlines, and snow flakes. However, not all self-similar objects are fractals—for example, the real line (a straight Euclidean line) is formally self-similar but fails to have other fractal characteristics. Fractals, when zoomed in, will keep showing more and more of itself, and it keeps going for infinity. (Full article...)

View all selected articles

edit

Subcategories

Full category tree. Select [►] to view subcategories.

More mathematics categories

edit

Topics in mathematics

General

Foundations

Number theory

Discrete mathematics

Algebra

Analysis

Geometry and topology

Applied mathematics

edit

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z